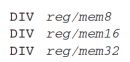728x90
Multiplication and Division Instructions
- 곱셈 나눗셈 명령.
1. MUL (unsigned multiply) Instruction(명령)
- Arithmetic 연산을 하면서 부호가 있는 것과 없는 것 들을 살펴봤다.
- 이 명령은 unsigned한 값들의 곱을 의미한다.
- 대부분의 Arithmetic 오퍼레이션은 피연산자가 2개였고 대부분이 바이너리 였다.
- 다만 이 명령은 특이하게도 피연산자를 하나만 받는다는 특징이 있다.
- 그렇다면 나머지 하나의 연산자는 지정이 되어있다는 뜻이다.
- 이 연산자는 피연산자가 메모리나 레지스터이다.
- 상수가 피연산자로 오지 않는다!
MUL명령의 3가지 버전

- 8비트의 피연산자가 있다면, 나머지 하나는 AL레지스터로 고정이다.
- 그 결과를 AX레지스터로 집어넣는다.
- 16비트인 경우에는 AX로 곱하고 결과값은 DX,AX레지스터에 위와 아래로 나뉘어서 들어가게 된다.
- 32비트의 경우에는 EAX로 피연산자가 지정된 상태이고 결과값은 EDX,EAX가 됩니다.
- 32비트 * 32비트는 64비트의 결과값을 내는것이다.
- 연산의 결과가 반으로 쪼개지는 것이 자세히 봐야할 부분이다.
- 왜 결과값을 반으로 쪼개는 걸까? (8비트 + 8비트면 eax 에 하면되는데? 라고 생각 할 수 있죠~)
- 그 이유는 이전 버전과 호환성을 위해서이다. (과거에는 16비트 레지스터가 없었기 때문에) 즉 역사적으로 호환성을 위해서 저런 형태의 명령을 가지게 된 것.
- 결과 값이 2배가 되는 이유는 자릿수가 절대로 넘어갈 수 없기 때문에 unsigned mul에서는 overflow가 발생할 수 없다.
- 간단하게 생각해보면
[1111] * [1111] < [1111/1111]예시를 보면 당연하다.(15 * 15 < 255) (= =225<255)
- 간단하게 생각해보면
- 그런데 곱셈의 결과로 오버플로우와 캐리플래그가 세팅된다.
- 엥 오버플로우 없다면서요?
- 네 맞아요 하지만 항상 세팅이 안되기 때문에 그 공간을 활용하고자 overflow의 세팅 의미를 바꿉니다.
- 따라서 여기서 세팅되는 overflow flag의 의미는 상위 레지스터를 봐도 되는가 아닌가를 보는것이다.
- 캐리플래그와 오버플로우는 같이 세팅된다. (동작 한다.)
- 즉 세팅이 되어있다는 건..! (=DX가 0이 아닌경우 ) 상위 레지스터를 본다라는 것을 의미합니다.
- 세팅이 안 되어 있다면.. 상위 반쪽을 안 봐도 된다는 뜻(상위 반쪽이 다 0이라는 의미)입니다.
- AL의 경우도 AX를 볼 때 AL만 보고 AR은 안 봐도 된다는 의미이다!
MUL 예시 1

- 8비트 8비트간 연산으로 AX에 결과값이 담기는데(AX = AR +AL) (이거 기억 안나면 복습!)
- CF가 0이므로 AL레지스터만 봐도 됩니다.
- 예시가 carry를 보는 이유(overflow가 아니라)
- 우리가 unsigned의 연산은 carry를 주로 보고,
- signed일때는 주로 overflow를 보기 때문에
MUL 예시 2

- 16비트 간 곱 예시이다. (결과값 16비트 + 16비트)
- DX와 AX에 잘려서 들어간 것을 볼 수가 있다.
- CF가 1이므로 DX와 AX를 모두 보고 해석해야 한다.
MUL 예시 3

- 32비트 간 곱 예시이다. (결과 (32 + 32비트)
- 이것도 보면 EDX와 EAX로 잘려 들어간 결과를 볼 수가 있다.
- CF가 0 이여서 EAX만 보면 된다.
2. IMUL (signed multiply) Instruction
- 이건 MUL의 signed 버전이다.
- 가장 큰 차이점은 부호값이다.
- 신경 써야 하는것이 항상 0으로 채워주는게 unsigned였지만 signed같은 경우 나머지 값을 1로 채워야하는 경우(음수)도 생기기 때문에 처리가 다르다.
- singed버전에는 명령어 앞에i가 붙곤 합니다.
- 3가지 종류의 singed mul이 있는데 피연산자의 갯수의 따라서 버전이 다르다는 특징이 있다.
2-1. 피연산자 1개인 경우 Single-Operand Formats
- 생긴게 unsigned버전과 같다.
- 역시 이것도 피연산자로 상수는 안된다.
- 8비트 8비트 곱해서 16비트 되는 등 연산의 결과가 2배씩 커지는게 같다.
- oveflow가 발생 할 수 없는 건 같다.
- carry flag와 overflow가 세팅이 앞의 절반을 볼지 말지에 대한 결정일 뿐이다.
2-2. 피연산자 2개 버전
- 결과 값으로 2배가 되는게 아니라 dest에 업데이트 하기 때문에 OVERFLOW 발생 가능!
- 어라 우린 앞에서 봤을 떄는 16비트끼리 곱해서 32비트가 됐기 때문에 다 저장이 됐었다.
- 근데 이건 16비트 16비트 곱해서 16비트가 되기 때문에 문제가 될수 있겠네?
- 그래서 넘치는 녀석들은 버려지게 됩니다. 하위만 16비트가 유지가 됩니다.
- 즉 그 말은 overflow가 발생할 수 있다는 것이다. (16비트를 넘어가는 케이스가 발생할 수 있다는 것이다.
- 앞에서는 앞쪽 레지스터를 볼지말지를 결정하는 flag가 이번에는 16비트의 범위를 벗어났는지를 나타내는 용도로만 사용된다.
- 예외사항 : 상수가 8비트가 껴있는 예외가 또한 이전에는 imm(상수)은 받지 않았지만 이 명령에서는 받을 수 있다.
2-3. 피연산자 3개 버전
IMUL Dest operand1 operand2
- Operand1 과 Operand2 를 곱해서 Dest에 넣어준다.
- 즉, 뒤에 있는 2개를 곱해서 dest에다가 넣어준다고 봄
- 무조건 Dest는 16비트 32비트 레지스터만 가능하다. 앞에 2개 버전과 dest의 제한 사항은 같다.

- 3개 다 사이즈가 같아줘야 한다. 다만 예외적으로 세번째 인자에 8비트 상수만 껴있다.
- 이것도 16비트 16비트 곱해서 16비트에 넣어주기 때문에 이것도 overflow와 carry flag가 세팅이 됩니다.
unsigned와 signed 결과값 예시
- 224 *3의 예시를 들어보면
- 이걸 바이너리로 곱해보면 224 = 1110,0000이 되고, 3은 0000,0011 이 된다.
- 이걸 곱해보면 1110,0000 + 1,1110,0000 = 10,1010,0000 즉 672가 된다.
- 이것이 1바이트에 들어갈까? 아니죠..!
- 그러면 512 + 160 해서 쪼개서 넣어주면 되겠죠.
- [10/1010,0000]
- 이걸 sign으로 보면 -32 * 3 = -96 이 나옵니다. ( 앞에 10 을 trunc하면 값이 같다진다.)
- 비트값으로는 [1010,0000]은 -96이고 결과는 truc만 하면 결과값이 같다!
- 이건 truc만 해주면 signed 연산을 unsigned의 연산이 같음을 볼 수가 있다.
- 다만 다른건 있는 비트를 어떻게 해석할지와 표현할 수 있는 숫자의 범위 뿐이지 연산 자체가 달라지지 않아도 된다.
- 따라서 IMUL연산이 unsigned에서 사용해도 문제가 없는 것이다! (다만 overflow와 carry flag는 주의해서 사용해야 한다.)
예시 1

- MUL연산과 헷갈려서 OF를 세팅 안해도 된다고 생각할 수 있지만 그렇게 하면 결과값이 엉뚱하게 나온다.
- 왜냐? 엉뚱하게 AL만 보게 되면 음수가 나오기 때문에 원하는 결과값이 아니게 됩니다.
예시 2

- 얘는 절반을 안봐도 된다…!
- 왜냐하면 oveflow가 발생하지 않았기 떄문이다.
예시 3
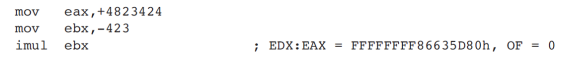
- 이걸 보고 하위 반쪽의 MSB가 상위 반쪽의 반쪽의 모든 부분을 채우고 있는가? 이걸 보고 signed extention임을 보면 된다.
- 지금까지 예시는 피연산자 1개를 취하는 예시였다.
예시 4

- 이 예시는 특별할 것 없는 예시입니다.
- 다만 2개의 인자를 받는 경우 어떻게 동작하는지 봐주면 된다.
예시 5 signed 거꾸로 overflow

- 16비트에 다 안 들어 간다.
- -32000은 [1000 0011 0000 0000] 이므로!!
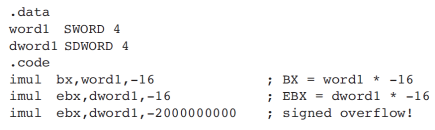
- 사실 담을 수 있는지 없는지만 확인 해보면 overflow세팅 여부를 알 수가 있으니 주의하자!
3. Measuring Program Execution Times
- 이 예제는 저자가 제공한 라이브러리에 있는 프로시저를 호출해서 사용하는 것이다.
- getmsceond를 호출하면 현재 시각을 아마 자정부터 현제 시간을 받아올 수 있다.
- 저자가 만든 getMseconds를 사용해서 시간이 얼마나 걸렸는지 보는 예제를 보여주는 것이다.

- 이게 갑자기 왜 나오냐..?
- 곱셈은 shift연산의 합으로 표현할 수 있다. 일반 곱셈명령과 곱셈간의 차이점을 보는 것이다.
- 곱셈 방법 36을 곱해주려면 32 + 4를 해서 곱해준다.
- 다만 그냥 하면 너무 컴퓨터가 빨라서 측정이 제대로 안 되기 때문에 루프를 돌려서 누적해서 힘을 힘들게 했다.
- 저자는 둘 간의 시간차이를 계산해보았다.
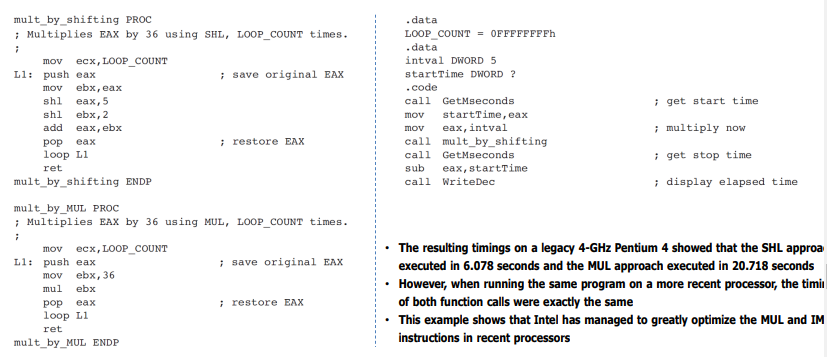
- 결국 저자의 결과값을 보고 MUL명령의 누적에 의해 속도의 차이가 발생했고, 하지만 인텔 CPU에서는 속도가 비슷했다.
- 이를 통해 알 수 있는건 인텔 CPU가 shift를 사용해서 곱셈을 optimize를 했다는 것을 예상해볼 수 있다.
4. DIV (unsigned divide) Instruction

- 나눠지게 될 녀석은 지정이 되어있다.
- 곱셈과 비슷하게 AX, DX:AX, EDX:EAX 를 레지스터나 메모리로 나눠준다.
- 몫은 AL, AX, EAX에 저장하고
- 나머지는 AH, DX, EDX에 저장된다.
- 생김새는 곱셈과 같이 생겼다.
- 나머지 값도 저장되는 것을 볼 수가 있다.
예제1,2

- 어디에 저장되는지 잘 보면 좋을 것 같다.
예제 3 32비트 나눗셈

- 반으로 쪼개는걸 보면 +4를 해주는게, 리틀앤디안이기 때문이다. 그 주소값을 찾기 위해서
- 즉 상위 반쪽을 찾으려고 +4 하위 반쪽은 아래부터.
5. Signed Integer Division
- 곱셈은 3개 였던 것과 달리 나눗셈에는 연산의 갯수가 1개이다.
- 아까는 16비트 나눗셈을 하려면 피젯수가 32비트였어야 했었고 8비트 나눗셈을 하려면 16비트가 필요했었다.
- 따라서 숫자를 채울 때 앞쪽에 잘라서 원래 붙혀줬는데 이것을 고려해서 signed extention으로 해야한다.
- mov sign익스텐션으로 추가 레지스터까지 채울 수가 없다.
- 그래서 인텔이 관련 명령어를 제공한다.
Sign Extension Instructions (CBW, CWD, CDQ)
- CBW(Convert Byte to word) : AL의 부호비트를 AH로 확장해서 숫자의 부호를 유지한다.
- CWD(Convert Word to Doubleword) : AX의 부호비트를 DX로 확장
- CDQ(Convert Doubleword to quadword) : EAX의 부호비트를 EDX로 확장한다.

- 이 명령 즉 signed extetion의 명령을 제외하면.. 따로 특별한 점은 없다.
- 한가지 생각해볼점 -100을 10으로 나누면 몫이 -6 나머지는 -10이다.
여기서 말하고 싶은건 나눠질 녀석과 나머지의 부호는 항상 같다.
- 과거에는 이렇게 계산하지 않고 다른 방식으로 나눗셈을 하는 계산법도 있었지만 표준에서 사라졌다.(몰라도 됩니다.)
생각해보기
- Q.) x86의 정수나눗셈에서 나머지의 부호가 피제수(dividend)의 부호를 따른다는 것과 달리, high level 프로그래밍 언어들(예: Python)에서는 제수(divisor)의 부호를 따르는 것 처럼 보인다 과연 왜 이런현상이 발생했을까?
- 정수나눗셈에서 나머지는 몫을 어떤 계산으로 구할 것인지에 따라 달라지게 됩니다. -100 / 15를 예시로 들면
- 몫을 truncation으로 구하는 방법은 -100 / 15에 대해서 몫과 나머지로 -6과 -10으로 도출해내고
- floor연산으로 구하는 방법은 몫을 -7과 나머지를+5로 도출합니다
- 그렇다면 프로그래밍 언어에서는 어떨까?
- C와 C++에서는 오래된 표준에서 이에 대해 정의하지 않아 컴파일러마다 구현이 달랐고, 이후의 표준에서 truncation 방식으로 정의됩니다.
- 대부분의 잘 알려진 프로그래밍 언어들(예: C, C++, C#, Java, JavaScript, Go, Objective C, PHP, SQL, Swift 등)이 truncation 방식을 따르고 있지만,
- 일부 언어들(예: Python, R, Ruby, Matlab 등)은 floor방식을 따릅니다.
예제
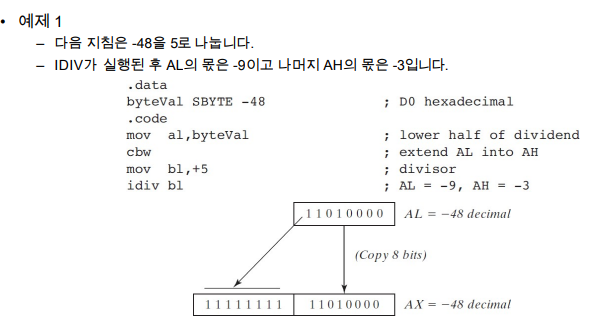
16비트 (EAX)최대 값은 0~65535 또는 -32768~32767이다.

- 이게 왜 확장이 되는지 자세히 봐야한다.!!
- 곱셈에서는 overflow와 carryflag가 세팅됐었다.
- 다만…! 나눗셈에서는 연산의 결과로써 flag레지스터 값이 어떻게 될지가 정의되어있지 않다.(제조사에서 지맘대로 할 수 있다.)
– Divide Overflow
- 나눗셈에서도 overflow가 발생한다..!

- AL은 1바이트 인데…! 2바이트가 결과값이므로 oveflow가 발생할 수 있다. (몫이 100이니까 결과값이 AL(4비트)에 저장되니까 overflow가 발생한다.
- 이렇게 나눗셈을 하면 프로그램이 종료가 된다.!!(overflow 플래그가 세팅되면 프로그램이 죽는다.
- 이런 에러를 방지하기 위해서는 큰 레지스터를 사용해라!!
6. Implementing Arithmetic Expressions
이건 어셈블러처럼 우리가 한번 해보는 것이다.(컴파일러처럼)
예시 1

예시 2

예시 3

neg : 음수로 바꿔준다.
이걸 시험문제에 낼 가능성이 높습니다!!!!!! 이걸 기본으로 따라가보세요!! 빈칸으로 낼 가능성 UP
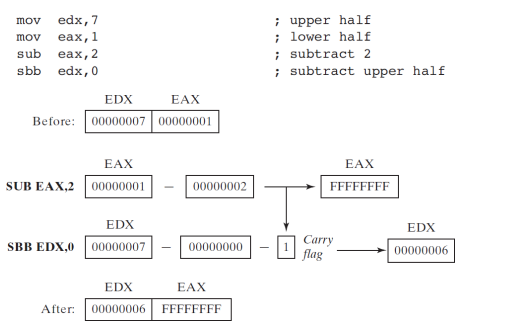
Extended Addition and Subtraction
1. ADC (add with carry) Instruction

- 이건 addtion이랑 거의 같지만.. 이건 carry까지 같이 더해준다.

- 여기서 1FE가 되는데 1은 truc가 된다.(carry로 나간다.)
- adc를 사용해서 더해주면.. 이전에 Carry가 1이 세팅 됐기 때문에 1이 된다.
- Carry flag를 말 그대로 더해주는 것이다!
- 피연산자의 크기는 동일해야만 한다.
2. Extended Addition Example
- 만약 5바이트 데이터를 만들어서 덧셈을 하고 싶을 때 어떻게 하면 될까?
- 여기서는 3바이트짜리를 덧셈하는 경우를 보여준다.

- 이 예제는 carry가 발생하지 않아서 3바이트 계산에서 캐리 발생했을 때 정상적으로 나오는 것을 봤을 텐데, 예제에서는 그렇게 있지 않다.
- L1중간에 pushfd를 해주는 이유는 carry flag를 저장하니까 왜냐면 add에서 carry flag를 건들기 때문이다.
- !!코드 중요!!!!!!
방금 만든 함수를 호출해줬다.
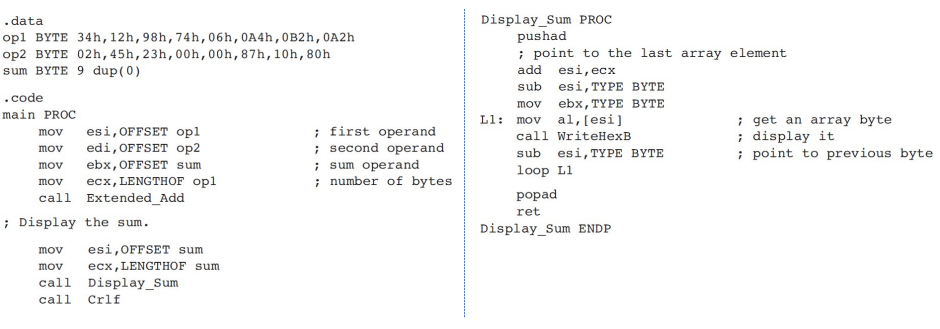
저기 L1은 리틀앤디안이 높은자리부터 낮은자리까지 루프 타면서 출력해주는 다는 것을 의미한다.
3. SBB (subtract with borrow) Instruction
- SBB는 dest에서 source와 carry값을 모두 뺀다.
- 사용 가능 피연산자는 ADC와 동일하다.
Uploaded by N2T
728x90
'CSE > system programing' 카테고리의 다른 글
| [시스템 프로그래밍 12-2강] Memory Management 페이징 기법 (0) | 2023.05.28 |
|---|---|
| [시스템 프로그래밍 12 -1강]advanced processor (Stack Frames) (1) | 2023.05.28 |
| [시스템 프로그래밍 10강] Shift and Rotate 명령 및 활용 (0) | 2023.05.16 |
| 9-2강 Conditional Control Flow Directives (조건부 제어 흐름 지시어) (0) | 2023.05.15 |
| 9 -1 강 Conditional Loop Instructions (LOOPZ,LOOPE) Conditional structure(조건부 구조 예시코드!) (0) | 2023.05.15 |