문제
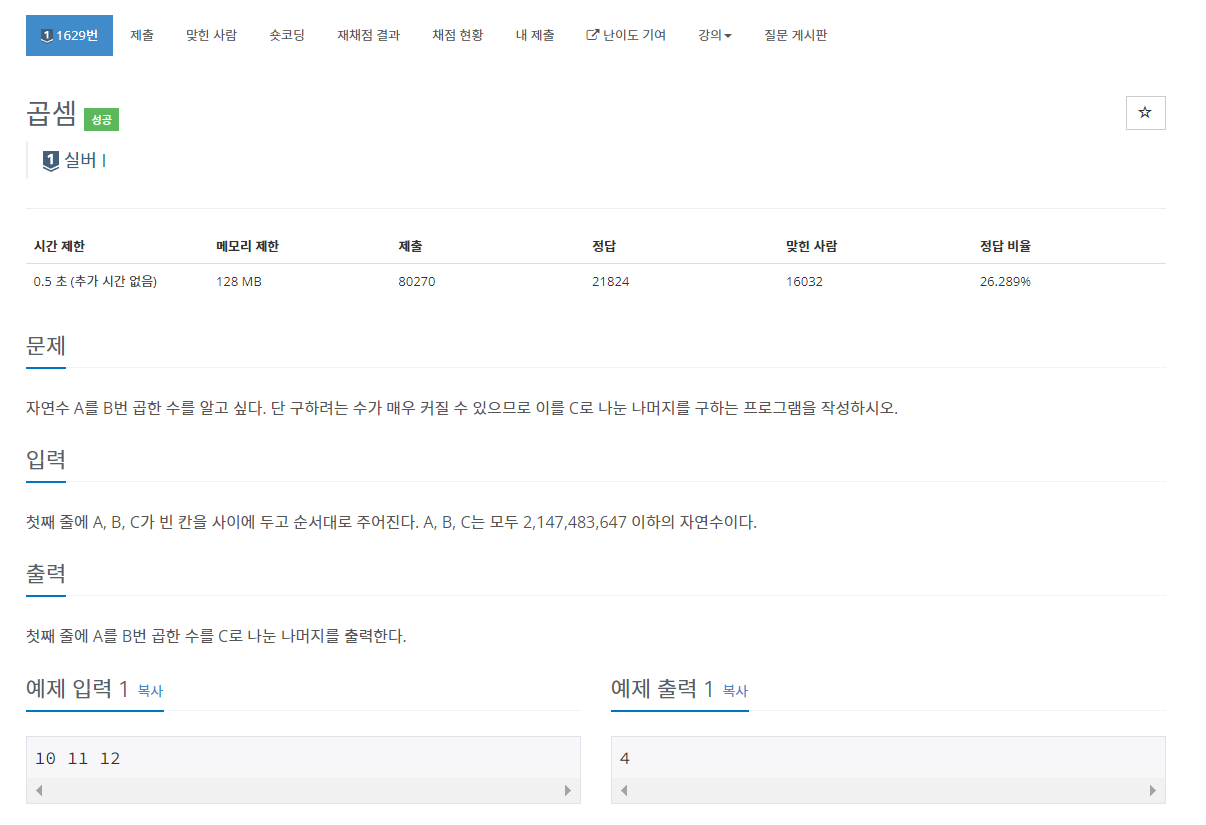
문제는 간단해 보이지만 쉽게 풀리지 않는다.
필수적으로 알아야 하는게 있는데
지수법칙 : a^(n+m) = a^n * a^m
모듈러 성질 : (a*b)%c = (a%c * b%c)%c
이 두가지를 알아야만 한다.
지수법칙은 아마 왠만하면 알 것 같은데 모듈러 성질은 곱해서 나누던 나눠서 곱하든 값은 같다는 것이다.
증명은 수학자들이 해뒀으니 위키백과를 보자.
그냥 구현 하면 시간초과 납니다.(왜 저 정답률이겠어요..)
정답 코드
#include <iostream>
#include <cmath>
using namespace std;
typedef long long ll;
int A,B,C;
ll p(ll x)
{
if (x == 1)
return (A%C);
ll k = p(x/2)%C;
if (x%2 == 0)
return (k * k % C);
else
return(k*k %C* A % C);
}
int main()
{
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
cin >> A>> B>> C;
long long ret = p(B);
cout << ret;
}처음엔 math헤더 쓰려했는데 나중에 보니 딱히 필요가 없었다.
문제 풀이의 흐름
- O(nlogn)시간 복잡도는 필요하다.
- 입력을 받는다
- 우리는 A를 B번 곱해준 값을 C로 나눈 나머지로 보여준다.
- 재귀를 이용해서 풀어서 시간 단축을 노린다.
- 우선 1이 되면 A의 나머지를 곱해준다.
- 아래로 가면 절반의 크기를 다시 재귀를 돌리고 절반의 크기만 돌리기 때문에
- 리턴할 때 K의 제곱으로 리턴을 해주는 것이다.
- 만약 짝수면 제곱만 해서 나머지를 리턴해주면 되고
- 홀수라면 한번 더 A를 곱해줘야되서 그렇게 분기를 시켰다.
주의 할 점
그냥 풀면 안되는 문제이다.
이런 짧은 문제가 더 맵다는 사실을 알고 더 집중해서 풀어야 겠다.
반성 및 고찰
#include <iostream>
using namespace std;
int main()
{
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
int A,B,C;
cin >> A>> B>> C;
int ret = 1;
for (int i=0; i < B;i++)
{
ret *=A;
ret = ret % C;
}
cout << ret;
}시간 복잡도 따위 고려하지 않고 코드를 짜게 되면 시간 낭비가 있을 수 있다.
조금 더 생각하고 코드를 짜도록 하자.
Uploaded by N2T
728x90
'알고리즘 > 백준-실버' 카테고리의 다른 글
| 백준 2178번 미로탐색 (C++) (0) | 2023.01.03 |
|---|---|
| 백준 4375번 1(C++) (0) | 2023.01.02 |
| 백준 3986번 좋은단어 (C++)(부제 맞왜틀..) (0) | 2023.01.02 |
| 백준 1940번 주몽(C++) (0) | 2023.01.02 |
| 백준 1213번 팰린드롬 만들기(C++) (0) | 2022.12.30 |

